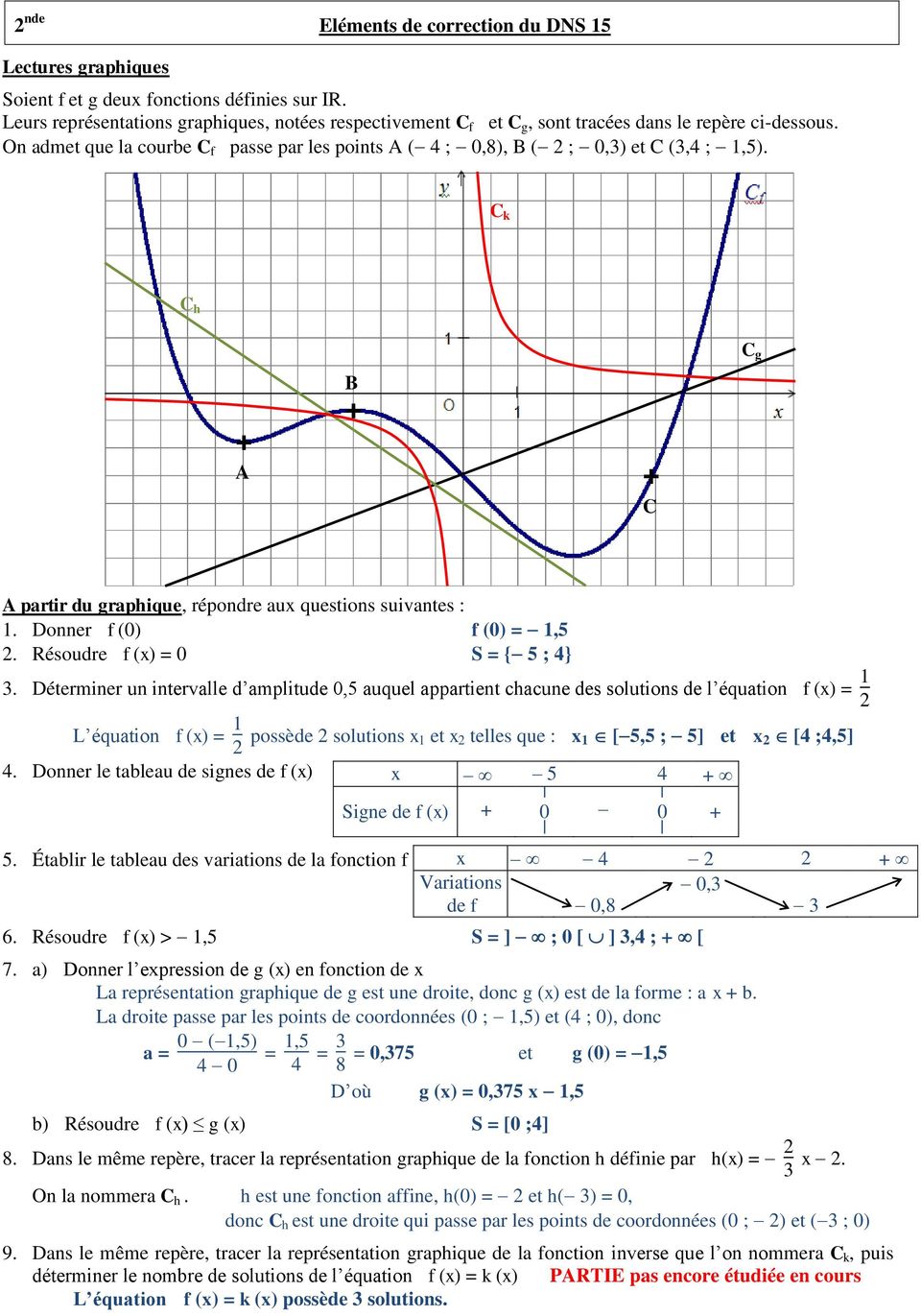
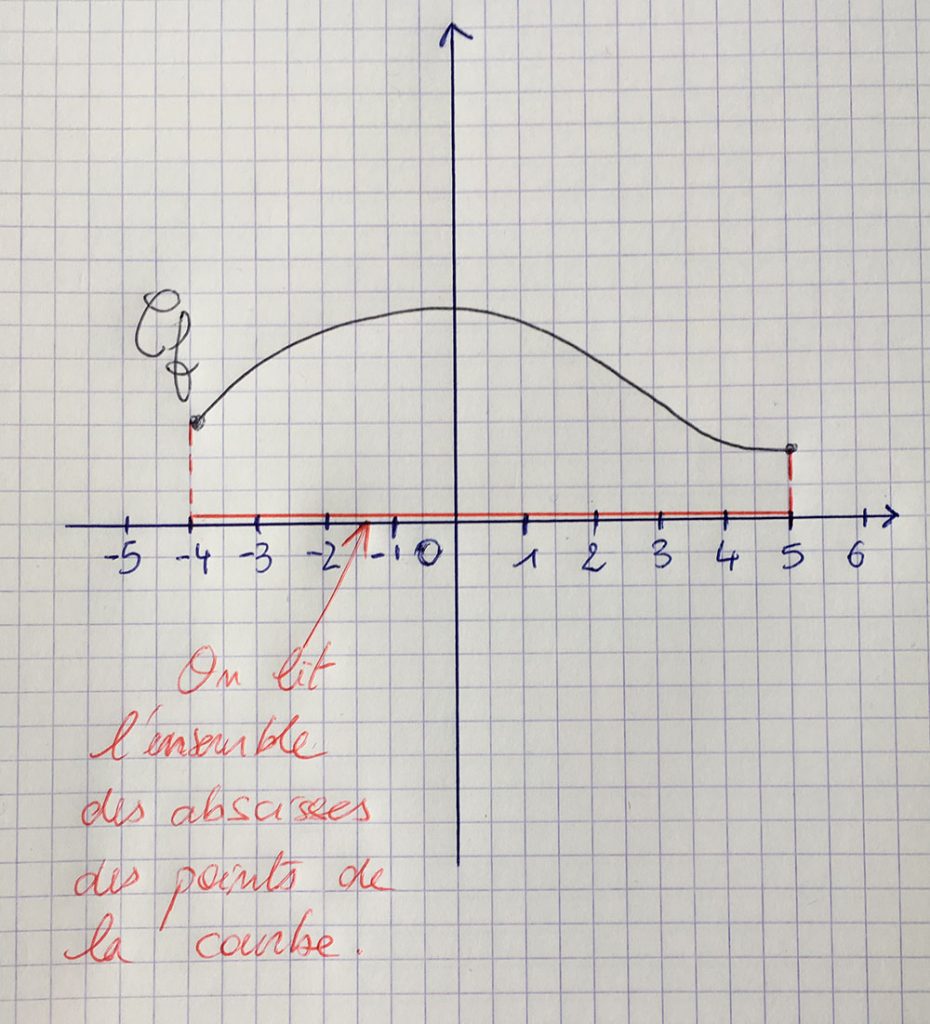
3,5;3,5 donc f 0 3,5 , f 2 3,5 , 3,5 3,5 Les solutions de l'équation f(x) = 3,5 sont x = 0 , x = 2 , x = –3,5 Résoudre l'équation f(x) = 0 graphiquement deux solutions a = 4 et x = 7 (car f 40 et fRépondre 1 on une question K K Exercice 1 Voici la courbe d'une fonction f définie pour des valeurs de x comprises entre 7 et 4 Déterminer graphiquement quand c'est possible a) L'image de 1 b) Un antécédent de 2 c) f(6) d) des antécédents de 1 e) un nombre qui a pour image 3 f) un nombre qui a pour antécédent 2 g) une solution de f(x) = 0 n 17 2 Exercice 2Il est possible de trouver les coordonnées à l'origine d'une fonction de deux façonsAlgébriquement ou Graphiquement Il suffit d'utiliser la règle de la fonction puis isoler y en remplaçant x par 0 Exemple à l'aide du graphique cidessus f (x)=axb f (x)=1 (0)3 f (x)=3 L'ordonnée à

Equations De Droites Fiche De Cours Mathematiques Schoolmouv
Déterminer graphiquement f(x)=0
Déterminer graphiquement f(x)=0-Une fonction f affine est définie sur ℝ par f (x)=mxp Si p = 0, f est une fonction linéaire Si m = 0, f est une fonction constante Exemples Je vous rappelle que vous devez être capable de refaire les exemples tout seul La fonction f définie sur ℝ par f (x)=−3x5 est affine car f (xUne fonction affine est représentée graphiquement par une droite qui n'est pas parallèle à l'axe des ordonnées Cas particuliers Si b = 0, f(x) = ax, f est une fonction linéaire et la représentation graphique est une droite passant par l'origine O Si a = 0, f(x) = b, f est constante et la droite est parallèle à l'axe des




Fonctions Polynomes Et Homographiques 1
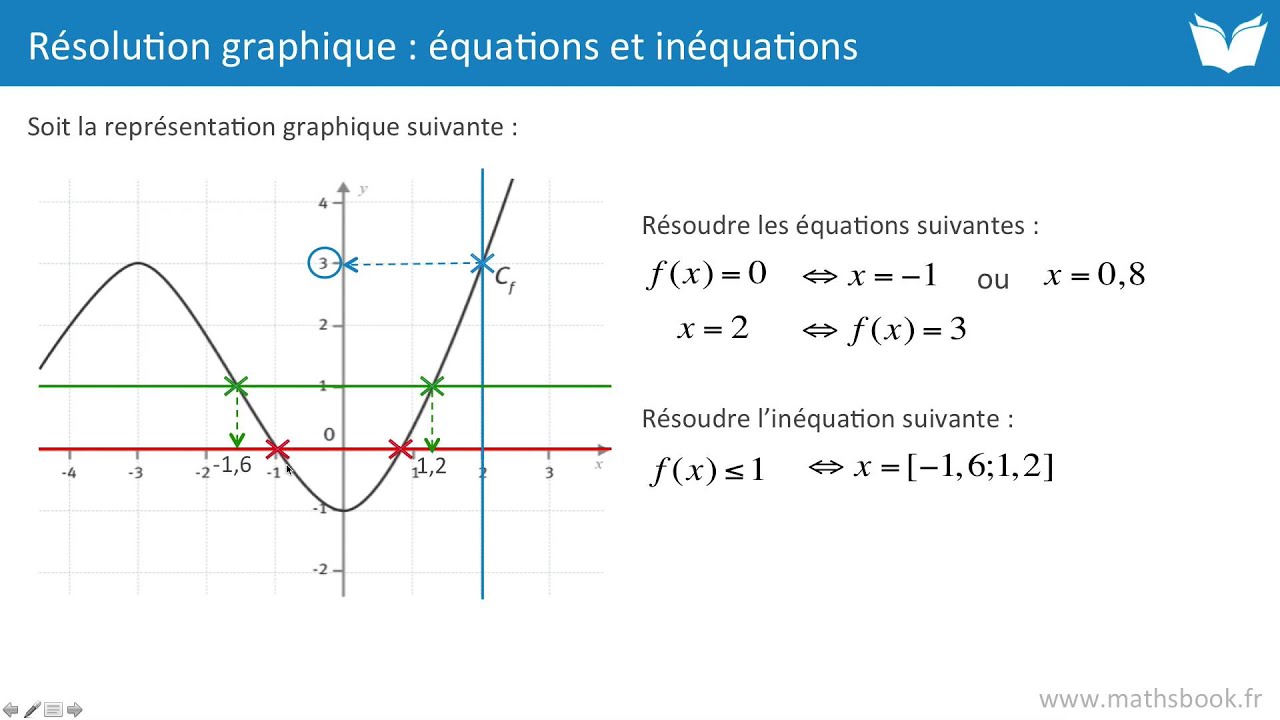
Résoudre graphiquement l'inéquation f(x)15 3 Résoudre graphiquement une équation Soit f et g deux fonctions défi nies sur une partie D de ˚ et (˚) et (˚') leurs courbes représentatives Soit k un nombre réel • Résoudre graphiquement dans D l'équation f(x)˚=˚k revient à déterminer dans D les antécédents de k par f, c'estàdire les abscisses des points de la courbe (˚) d'ordonnée égale à k2nde Résolution d'équations et d'inéquations (f(x) 0, f(x) g(x), f(x) metc) graphiquement et par le calcul Notamment, savoir déterminer le signe d'une expression au moyen d'une factorisation suivie d'un tableau de signe Objectifs du chapitre en terme de TICE
Page 1 / 2The tangent line is just the line itself So f' would just be a horizontal line For instance, if f (x) = 5x 1, then the slope is just 5 everywhere, so f' (x) = 5 Then f'' (x) is the slope of a horizontal linewhich is 0 So f'' (x) = 0 See if you can guess what the third derivative is, or the fourth!F x sin 5x 2 et f x sin x et f x sin2xcos3x et f x 3 tan 3x et f x x 3sinx 2 4 2 f x x et f x x et f x x 7x 12 et f x x 7x 12 2 2 3 Etudier la dérivabilité de la fonction f au point x 0 1 a x1 0 fxavec x x 2x 12 x1 f 0 1 ° ® ° ¯ b x0 0 avec ° x 1 1 x fx x f 0 0 ° ® ¯ c avec 3 2 f x 7x 1 , x 0 3x 1 f x , x 0 x1 °
2x 3 x 4 Résoudre graphiquement f(x) 0 La valeur interdite semble être 4 et il semble que l ensemble des solutions soit S 4 1,5 Résoudre par le calcul f(x) 0 x 4 0 x 4 La valeur interdite est 4 f(x) 0 2x 3 x 4 0 On construit un tableau de signes en procédant comme pour le produit, à l exception des 0 sur la dernière ligneThe limit as x>0 from the right of sqrt (x) is 0 However, limit as x>0 from the left of sqrt (x) is does not exist, and since the limit from the left does NOT equal the limit from the right, then the limit from both sides does not exist Conversely, the limit as x>1 from the right of sqrt (x) is 1 And, limit as x>1 from the left of sqrtExercice de maths corrigés




2 Fonctions2 Exos Fonction Mathematiques Algebre Generale




Td Maths Les Items E De L Incomprehension Ue4 Biostatistiques Tutorat Associatif Toulousain
Dans le cas particulier de l'équation f(x) = 0, les solutions sont les abscisses des points d'intersection de la courbe avec l'axe des abscisses Exemple La courbe cidessus représente une fonction f L'ensemble des solutions de l'équation f(x) = 4 est S = {−2 ;Oct 09, 09 · Voila, je suis en 1ere S et ma prof de maths viens de me donner un DM mais je n'arrive pas a résoudre f (x)=0 Voila l'équation f (x) = x/x²92Dans toute la suite on écrit f(x) 2x 4 Résoudre graphiquement dans R l'inéquation 2x 4 0 3aTracer dans le même repère la droite représentation graphique de la fonction affineg(x) x 5 bRésoudre graphiquement dans R l'équation f(x) g(x) cRésoudre dans R graphiquement l' inéquations f(x) g(x) figure 1



Representation Graphique Des Fonctions




Bonsoir Je Bloque Sur 2 Exercice Pour 1 Exo 8 Le Plan Est Rapporte Au Repere Orthonormal Nosdevoirs Fr
1 a b0 = 2 400 ;F > >x 0, ;Définition Une fonction est dite « affine par morceaux » lorsqu'elle est définie sur des intervalles de ℝ par différentes fonctions affines




Fonction Affine Wikipedia




Resolution Graphique De F X 0 Sur Calculatrice Graphique Texas Instruments Avi Youtube
Nombres De Solutions D Une Equation 1 Resoudre Graphiquement A F X 3 B F X 5 C F X 0 D F X Ppt Download For more information and source, see on this link httpsAug 22, 18 · This says that the gradient vector is always orthogonal, or normal, to the surface at a point So, the tangent plane to the surface given by f (x,y,z) = k f ( x, y, z) = k at (x0,y0,z0) ( x 0, y 0, z 0) has the equation, This is a much more general form of the equation of a tangent plane than the one that we derived in the previous sectionIf F(x)=x has no real solution then also F(F(x)=x has no real solution



Equations Et Inequation Avec Graphique 2 Reponses Lycee Forum De Mathematiques Maths Forum




Calameo Ds Sur Les Fonctions
A) f(x) = 0 b) f(x) = g(x) c) f(x) ≥ g(x) 3) Interpréter graphiquement les résultats de la question 2 Approfondissement 6 Fonction affine par morceaux ?B1 = 2 400 x 0,8 = 1 9 b La suite (bn) est une suite géométrique de raison q = 0,8 c bn = b0 x q n = 2 400 x 0,8n Le nombre de bactéries restantes au bout de 5 h est d'environ 786 400 2 a 0,8 < 1, et 2 400 > 0 donc la fonction f est décroissante Tableau de variation voir cicontre b Graphiquement le nombreWwwmathsenlignecom XERCICES FONCTIONS NUMERIQUES D'UNE VARIABLE REELLE E 9A C ORRIGE – NOTRE DAME DE LA MERCI MONTPELLIER EXERCICE 9A1 Les courbes C f, C g, C h et C k qui représentent les fonctions f, g, h et k j a Résoudre graphiquement les équations f (x) = 3 si x = 1 ou x = 2 g(x) = 2 si x = 3 ou x = 3 h(x) = 3 si x = 3 k(x) = 4 si x = 4 ou x = 1




Limite Et Derivee Graphiquement Youtube




Comment Trouver L Equation D Une Droite Tangente
Algebra Graph f (x)=0 f (x) = 0 f ( x) = 0 Rewrite the function as an equation y = 0 y = 0 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope andFor example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1 / f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domainX 1 x 3 x 0 7 Déterminer graphiquement g 0,> f > 8 On déduit la monotonie de fg sur > 0, f 9 Donner le tableau de variations de la fonction 08 On considère la fonction définie par x92 fx x 1 Déterminer domaine de définition de la fonction 2 Montrer que la fonction est impaire 3 a Soit x et y de * tel
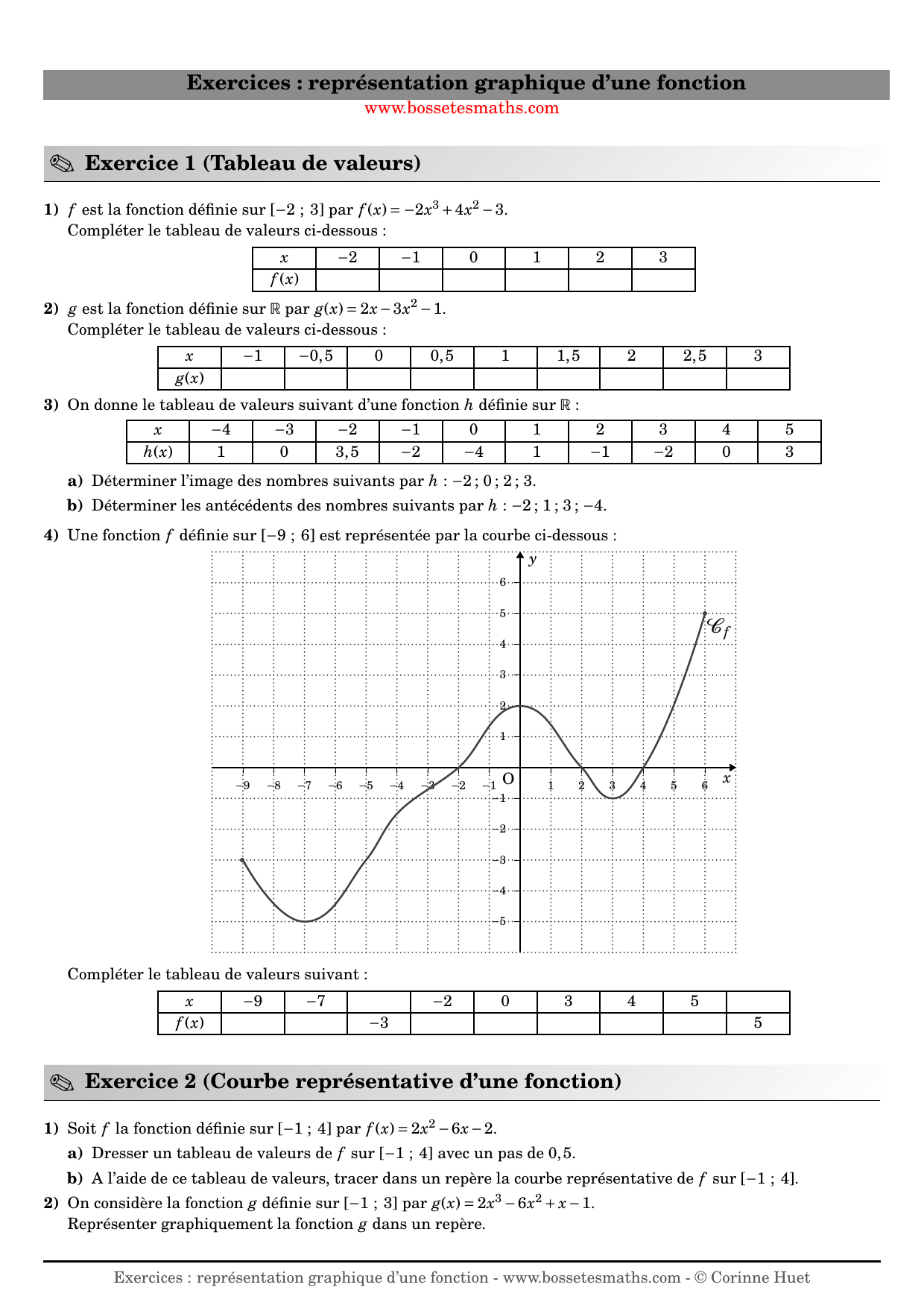



La Feuille D Exercices Sur La Representation Graphique D Une Fonction
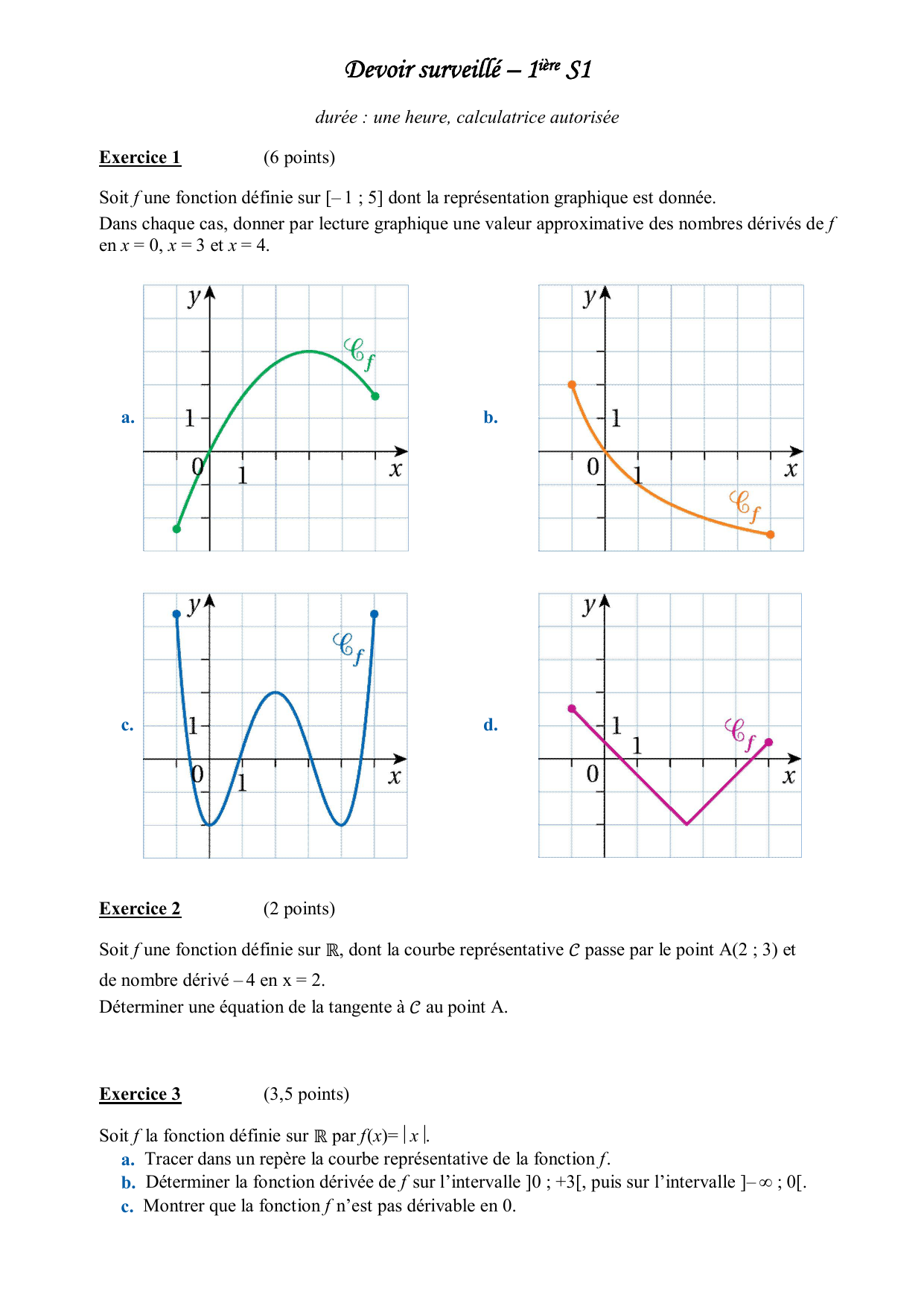



Devoir Surveille 1iere S1
9 onionc tfa L f est définie par f (x) = 2 x2 3 pour x compris entre 1 et 2 1 Recopier et compléter le tableau cicontre 2 Tracer la courbe représentative de f dans un repère x 1 0,5 0 0,5 1 1,5 2 f(x) 8 Tracer la représentation graphique de la fonction g définie par g (x) = 2 x x2 pour xX définie par f x x x 2 2 ① a Déterminer D f l'ensemble de définition de la fonction f b Calculer lim x fx f ② Etudier la dérivabilité de f en 0 à droite et interpréter le résultat graphiquement ③ a Calculer fx ' pour tout xD f ^0` b Etudier les variations de f ④ apour tout Calculer fx''Dec 21, 13 · bonjour, résoudre f (x)=g (x) soit ( f − g) ( x) = 0 On recopie, et on range x 2 − 2 x − 3 − 2 x 7 = 0 soit x 2 − 4 x 4 = 0 tu trouve le discriminent, et tu calcules les éventuelles racines Ensuite tu vérifie qu'elles sont cohérentes avec le problème initiale edit Comme l'a dit holomos, il y a surement une belle mise




Bonsoir Pouvez Vous M Aider Sur Cet Exercice S Il Vous Plait En Utilisant La Representation Nosdevoirs Fr




Lecture Graphique De Fonction Derivable
Resoudre Graphiquement F X G X 2nde Exercice Mathematiques Kartable For more information and source, see on this link https Derivation Resoudre Graphiquement Et Par Le Calcul F X 0 Lire F A Important Youtube For more information and source, see on this linkDec 03, 16 · Suppose $f''=f$ and consider $g(x)=(f'(x)f(x))e^{x}$ Then $$ g'(x)=(f''(x)f'(x))e^{x}(f'(x)f(x))e^{x}=0 $$ Therefore $g(x)$ is constant Since $$ g(0)=0 $$ we have $f'(x)f(x)=0$, for every $x$ Therefore $f'=f$ Consider $$ h(x)=f(x)e^{x} $$ Then $h'(x)=f'(x)e^xf(x)e^x=0$ so also $h$ is constant Since $h(0)=0$, we are doneLire graphiquement les variations ou le signe d'une fonction sur un intervalle Calculer en fonction de a et de b, pour quelle valeur de x, on a f(x) = 0 En observant les résultats obtenus cidessus, énoncer une conjecture sur le signe de f selon les valeurs de x
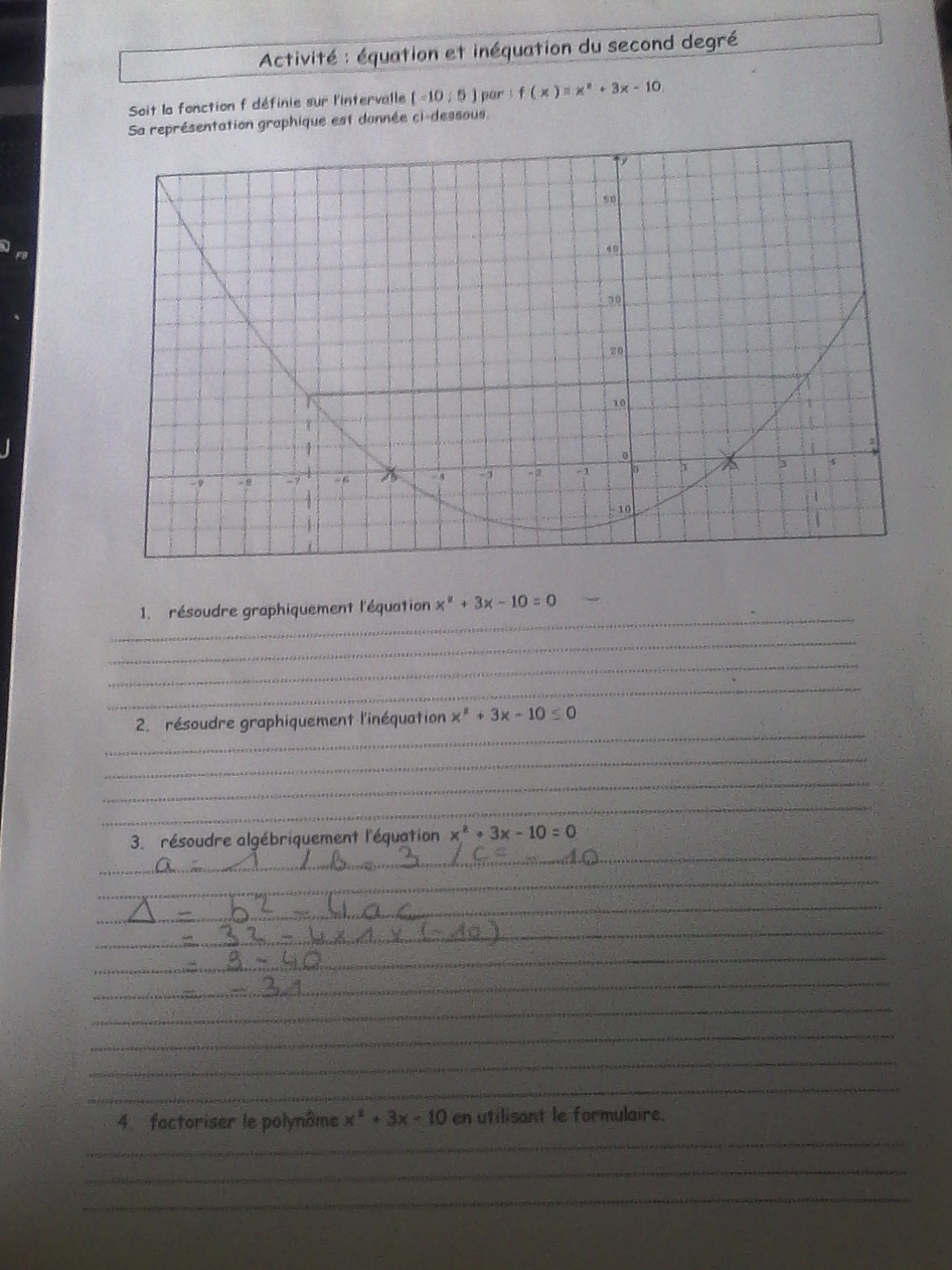



Activite Equation Et Inequation De Second Degres Digischool Devoirs




Fonctions Affines Table Des Matieres Pdf Telechargement Gratuit
Nombres De Solutions D Une Equation 1 Resoudre Graphiquement A F X 3 B F X 5 C F X 0 D F X Ppt Download For more information and source, see on this link httpsGraphiquement on lit braceleftbigg f (0) = 4 f ′ (0) = 0 3 On a f (0) = a b et f ′ (0) = 1 − b D'où braceleftbigg a b = 4 1 − b = 0 ⇐⇒ braceleftbigg a b = 4 1 = b ⇐⇒ braceleftbigg a = 3 1 = b Donc f (x) = x 3 e − x 4 On sait que lim x →∞ e − x = 0, donc lim x →∞ f (x2nde Résolution d'équations et d'inéquations (f(x)=0, f(x)




Bonsoir Besoin D Aide 1 Preciser Si Les Affirmations Sont Vraies Ou Fausses A F 5 Lt Nosdevoirs Fr




Coucou Je Dois Resoudre Graphiquement 1 F X 0 2 F X 3 F X Gt 1 Merci De Me Repondre Si Nosdevoirs Fr
Solution f(x)=0 ⇔ x=1/2;Déterminer graphiquement l'expression de la fonction affine dont on a tracé la courbe j = –0,5 3 f (x) = x 2,5 f (x) = 0,5Les solutions de l'équation f(x) = g(x) sont les abscisses des points d'intersection des deux courbes Cf et Cg Les solutions de l'équation f(x) = g(x) sont donc S = {x1;x2} Résolution graphique des inéquations 1er cas 1er cas inéquations du type f(x) ≥ k où k appartient à ℜ




Convexite Et Lecture Graphique Continuite Derivation Lectures Graphiques Et Convexite Fiche Exercices Maths Terminale Es 19




Bonsoir J Ai Un Devoir De Math A Remettre Et Je Suis En Difficulte Pourriez Vous M Aider Svp Soit Nosdevoirs Fr
/ 0 f x 0 La tangente T est Interpréter le résultat graphiquement Réponses 1 D ,1 f f@ @ 2 a) 3 1 3 x1 3 3 x1 3 2 x1) 1 im 1 x im x1 1x im 1 x1 1 im 1 x1 oo o o o f b) admet une demitangente verticale à gauche du point 1 dirigée vers le bas IVSur le graphique cicontre, on voit que l'équation \(f(x)=g(x)\) a deux solutions égales approximativement à 1,1 et 4,4Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
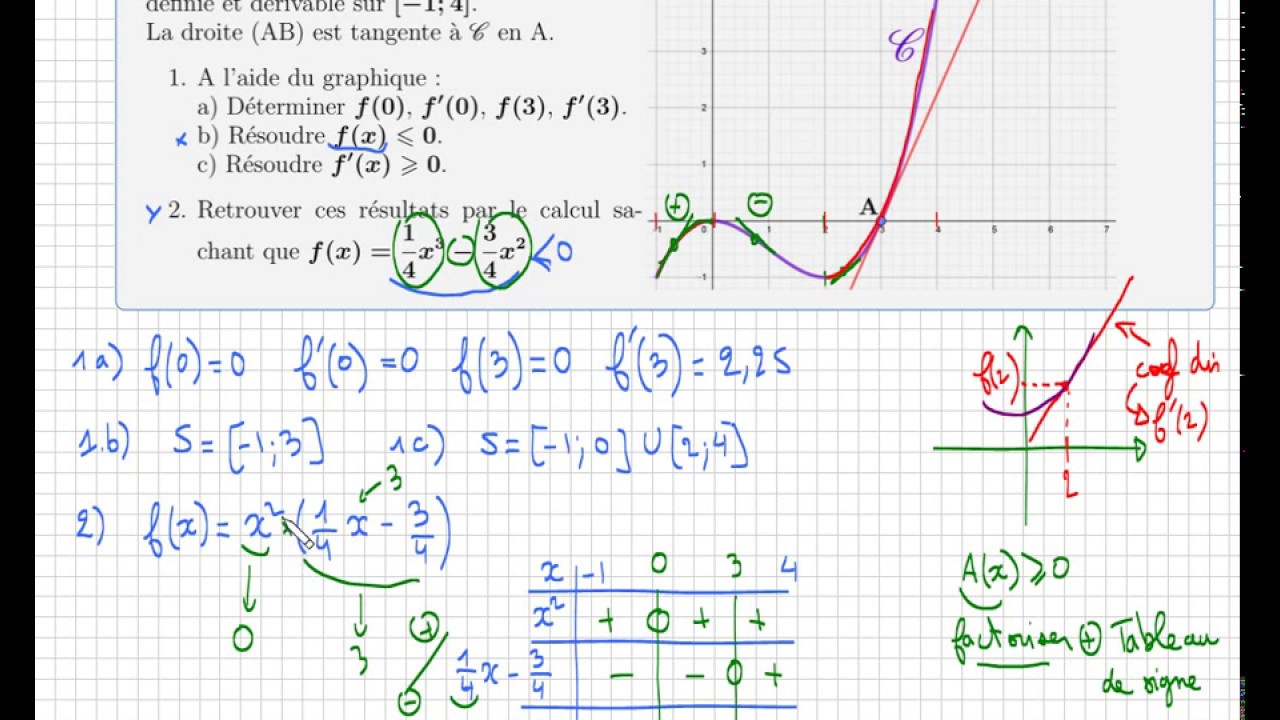



Derivation Resoudre Graphiquement Et Par Le Calcul F X 0 Lire F A Important Youtube




Equation De Tangente Par Lecture Graphique Pdf Cours Exercices Examens
(On donnera un tableau de valeurs bien choisies) 4°) Résoudre l'équation f ( x )=0 , graphiquement, et par le calcul 5°) Résoudre l'inéquation f (x )>4 , graphiquement, et par le calcul 6°a) Comparez sans les calculer les images de – π et de – 3,14 par la fonction fFonctions Resoudre Graphiquement Une Equation Exercice N 1 Exercices D Entrainement En Mathematiques 2nde Reussirenclasse Com Service De Soutien Scolaire En LigneMar 10, 10 · Graphiquement,l'équation f'(x)=0 admet une solution qui est l'abscisse des points d'intersections de la tangente avec l'axe des abscisses On obtient donc pour solutions un nombre0 Deuxième partie




Ex 52 On Considere Deux Fonctions F Et G Definies Par Nosdevoirs Fr




Fonctions Resolution Graphique D Equations F X K Youtube
Soit la fonction linéaire f définie par f(x) = – x • Sa représentation graphique est une droite D qui passe par l'origine • Pour construire D , il suffit de déterminer les coordonnées d' un autre de ses points, c'estàdire un nombre et son image par f




La Fonction Cube Fiche De Cours Mathematiques Schoolmouv




Quelq Un Pourrait M Aider S Il Vous Plait On Considere Une Fonction F Definie Sur 8 3 Dontla Nosdevoirs Fr




Fonction Lineaire Analyse Wikipedia




La Fonction Inverse Fiche De Cours Mathematiques Schoolmouv
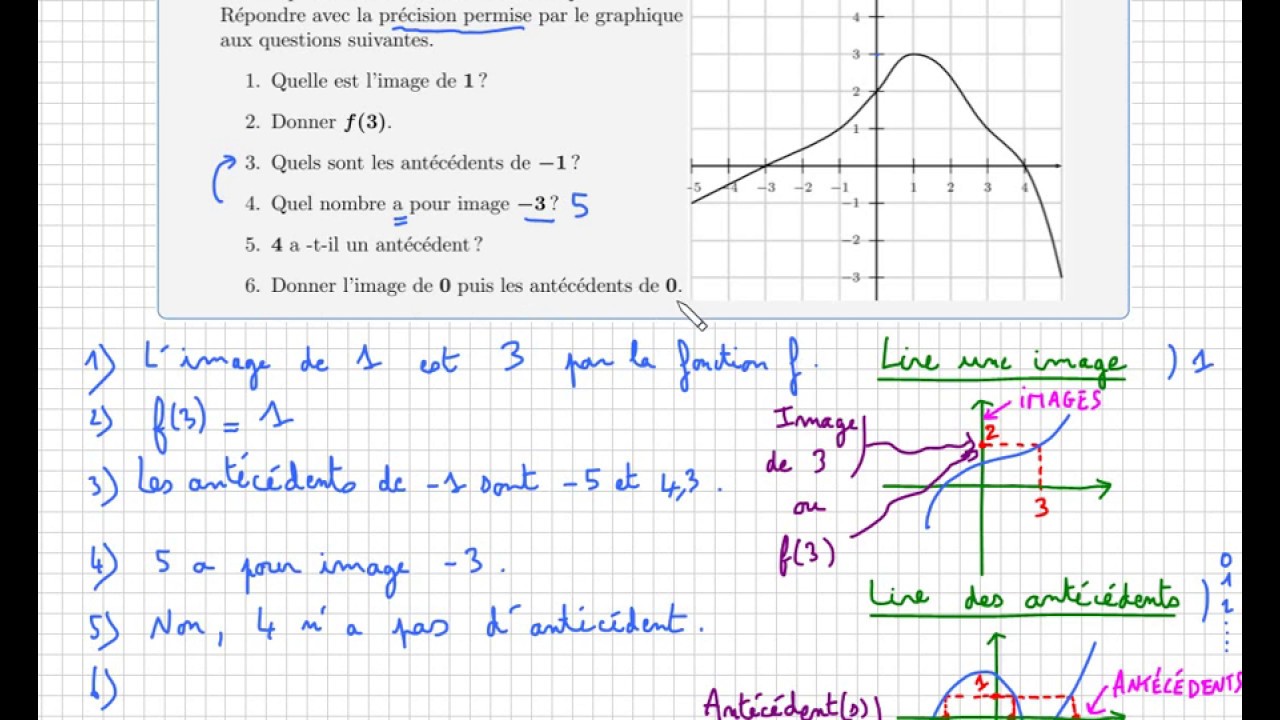



Fonction Lire Image Et Antecedents Graphiquement Troisieme Seconde Courbe Youtube
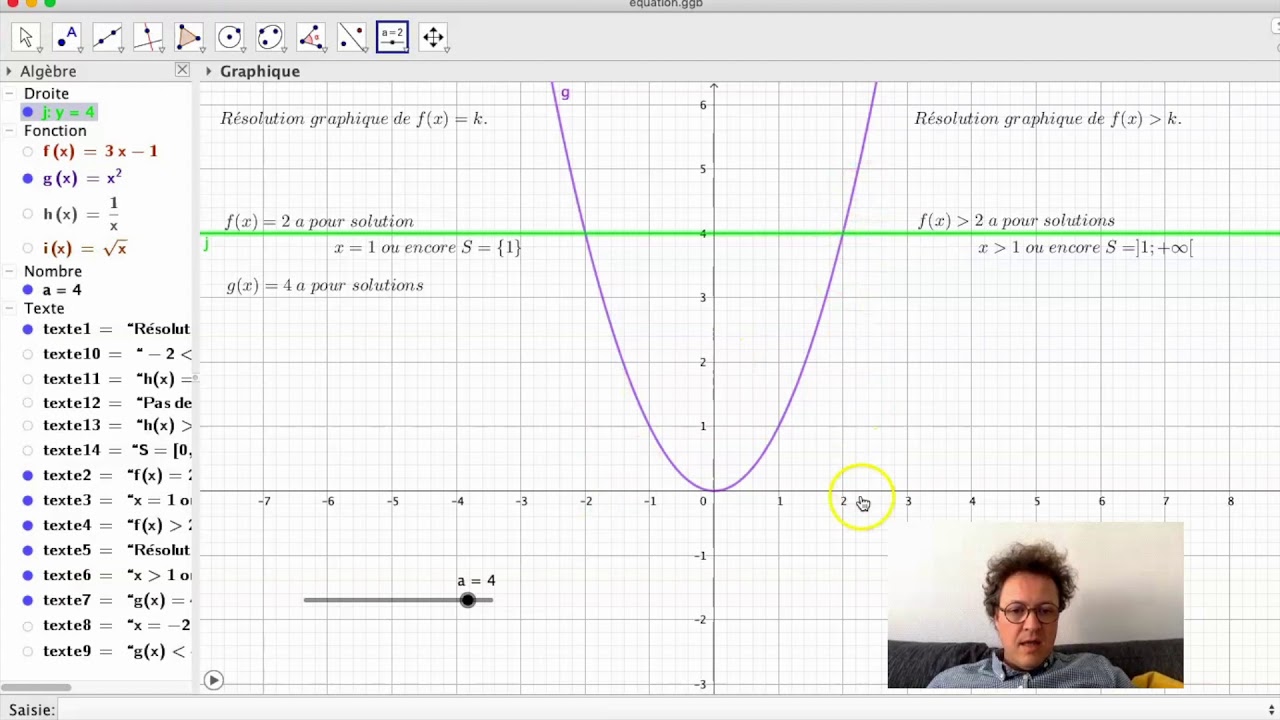



2g Representer Algebriquement Et Graphiquement Les Fonctions Mathematxlab




Bonjour Determinez Graphiquement F 0 F 1 F 2 Merci Pour Votre Aide Car Je Ne Sais Pas Du Nosdevoirs Fr
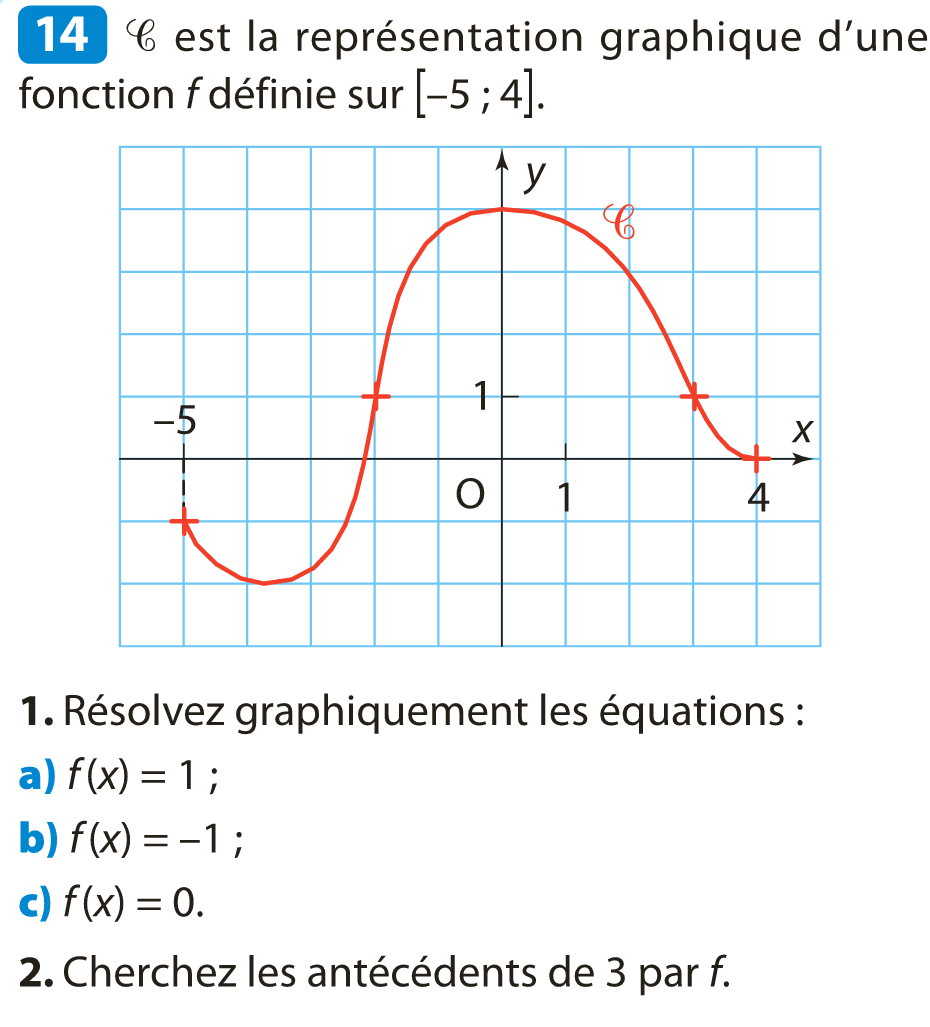



Exomorphisme



Limite D Une Fonction Definition Asymptote



Resolution Graphique D Equations Et D Inequations Cours De Maths Youtube




Equations De Droites Fiche De Cours Mathematiques Schoolmouv




Fonction Resolution Graphique Fonction Affine Pdf Free Download




Notion De Fonction Resolution Graphique Fonction Affine Pdf Free Download




Resoudre Graphiquement Une Equation Du Type F X K 2nde Exercice Mathematiques Kartable



Fonctions Numeriques Et Generalites Cours De Maths En 2de



Suite Recurrente Visualisation Graphique Geogebra



C K A C X Signe De F X X Variations Pdf Telechargement Gratuit




Determiner Graphiquement La Valeur De F A 1ere Methode Mathematiques Kartable
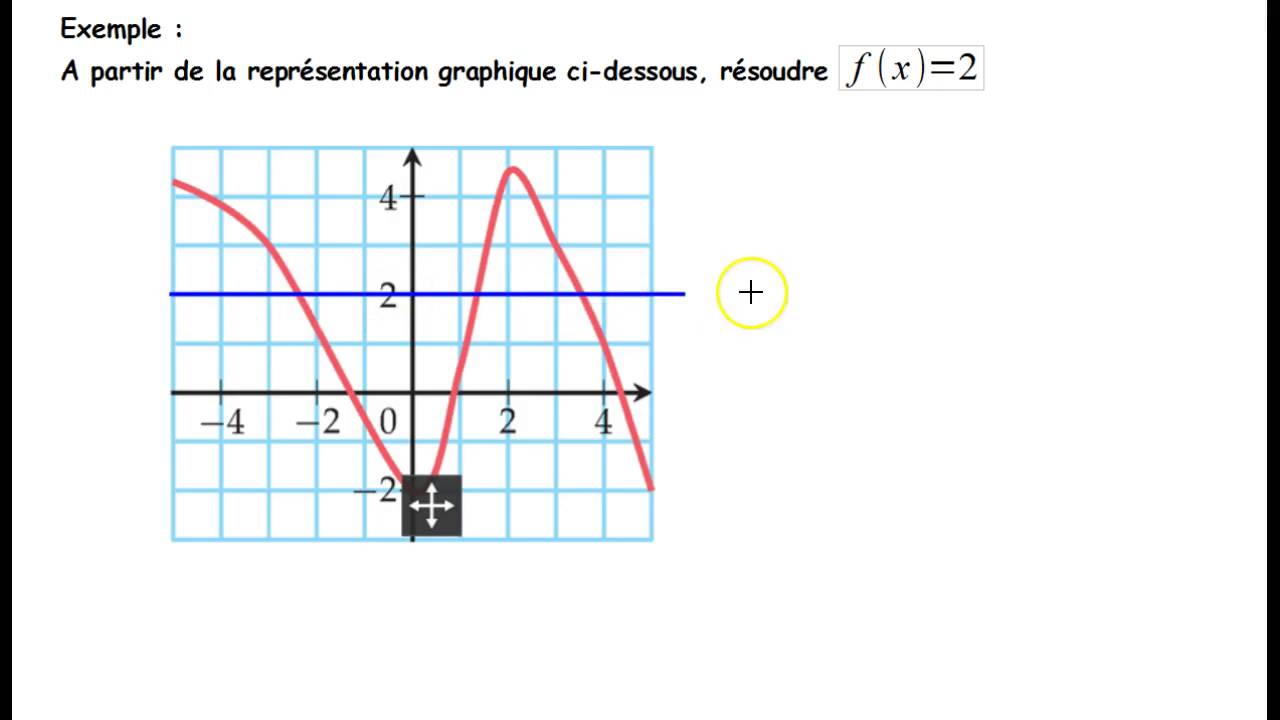



Resoudre Graphiquement F X K Youtube
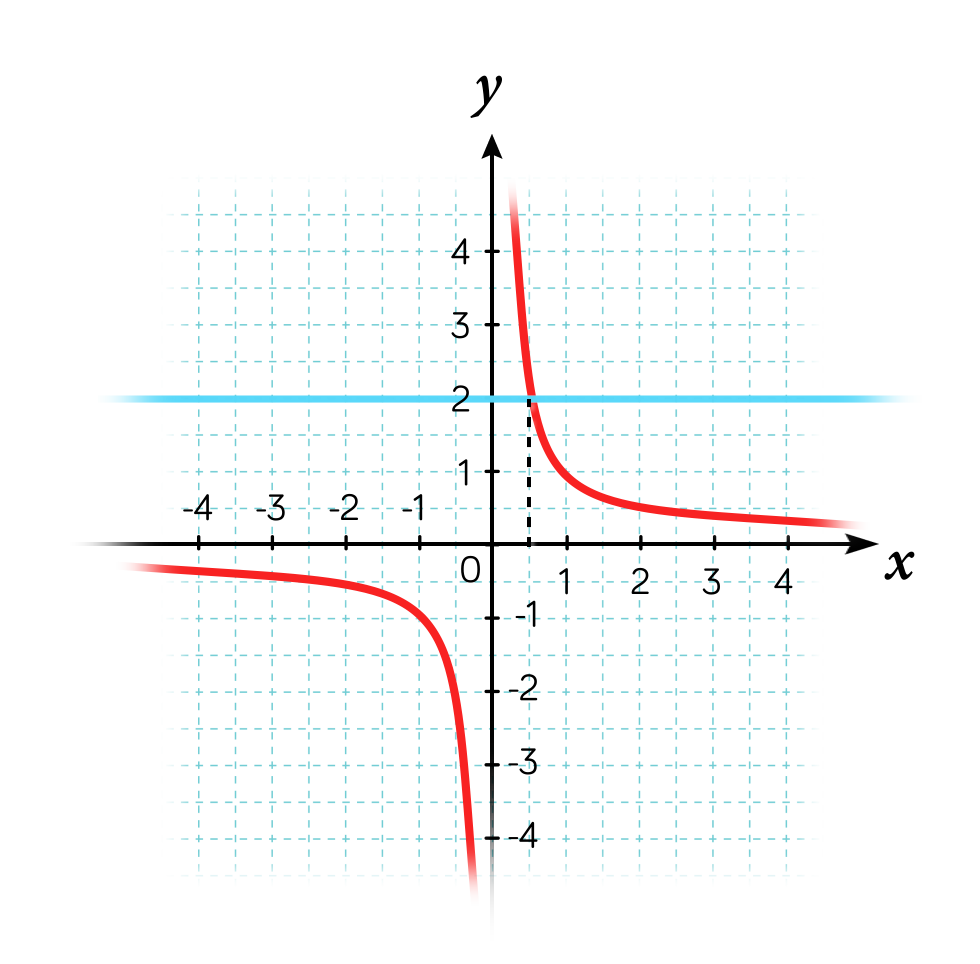



La Fonction Inverse Fiche De Cours Mathematiques Schoolmouv
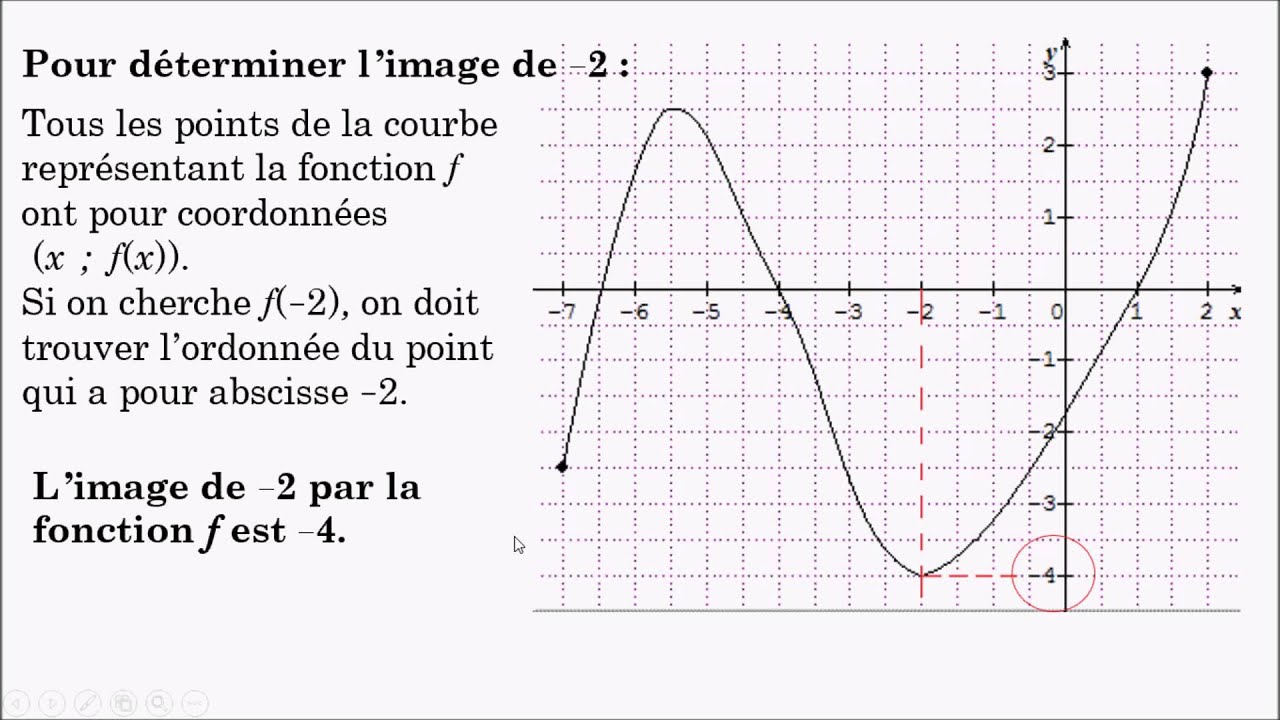



F5 Lecture Graphique D Une Fonction Youtube




Suite Recurrente Convergence Divergence Graphique Geogebra




Comment Determiner Graphiquement La Valeur D Un Nombre Derive D Une Fonction Youtube
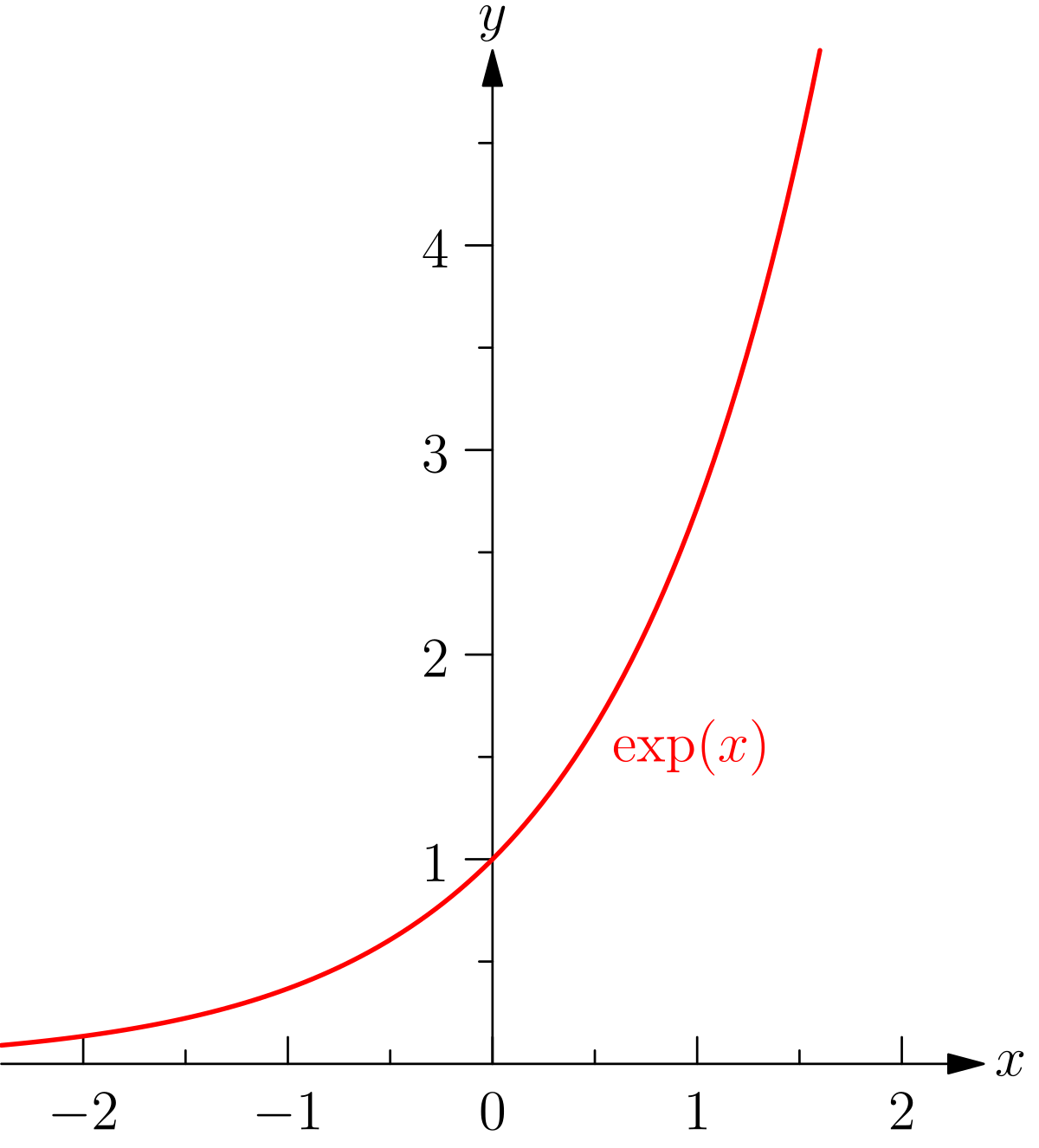



Fonction Exponentielle Wikipedia



Classe De Seconde Determiner L Ensemble De Definition D Une Fonction Cours Thierry
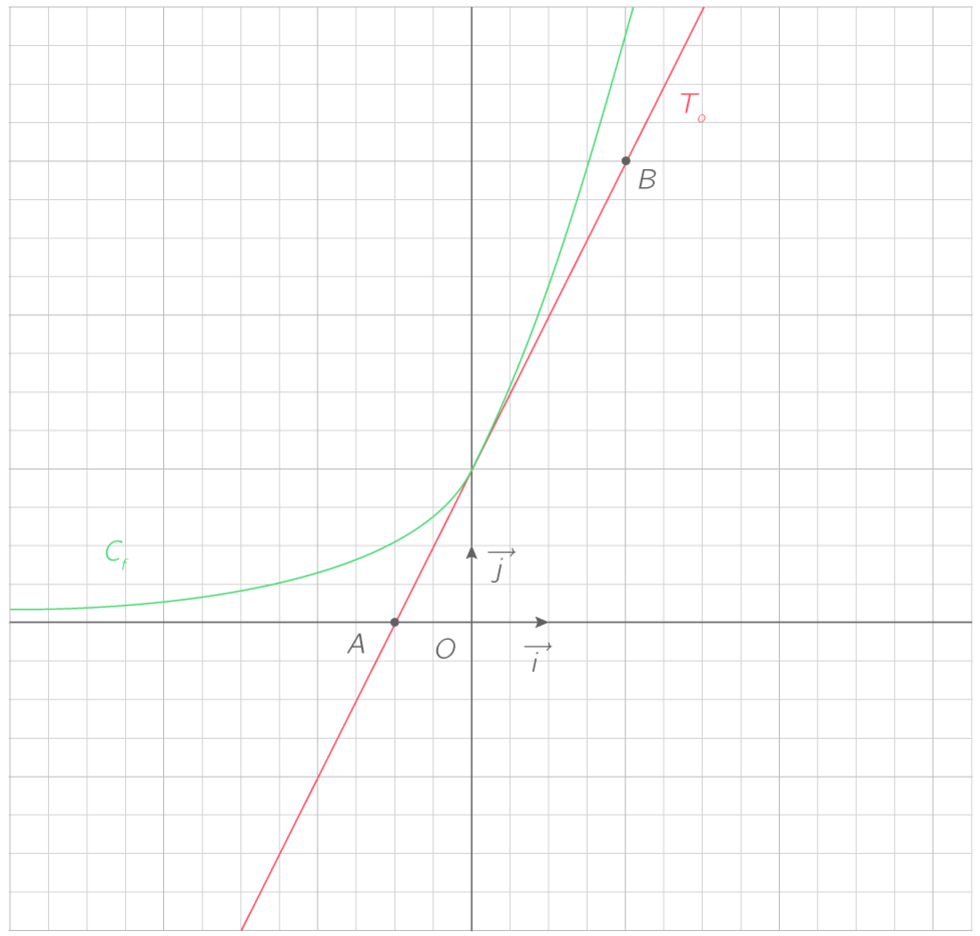



Determiner Graphiquement La Valeur De F A Cours Terminale S
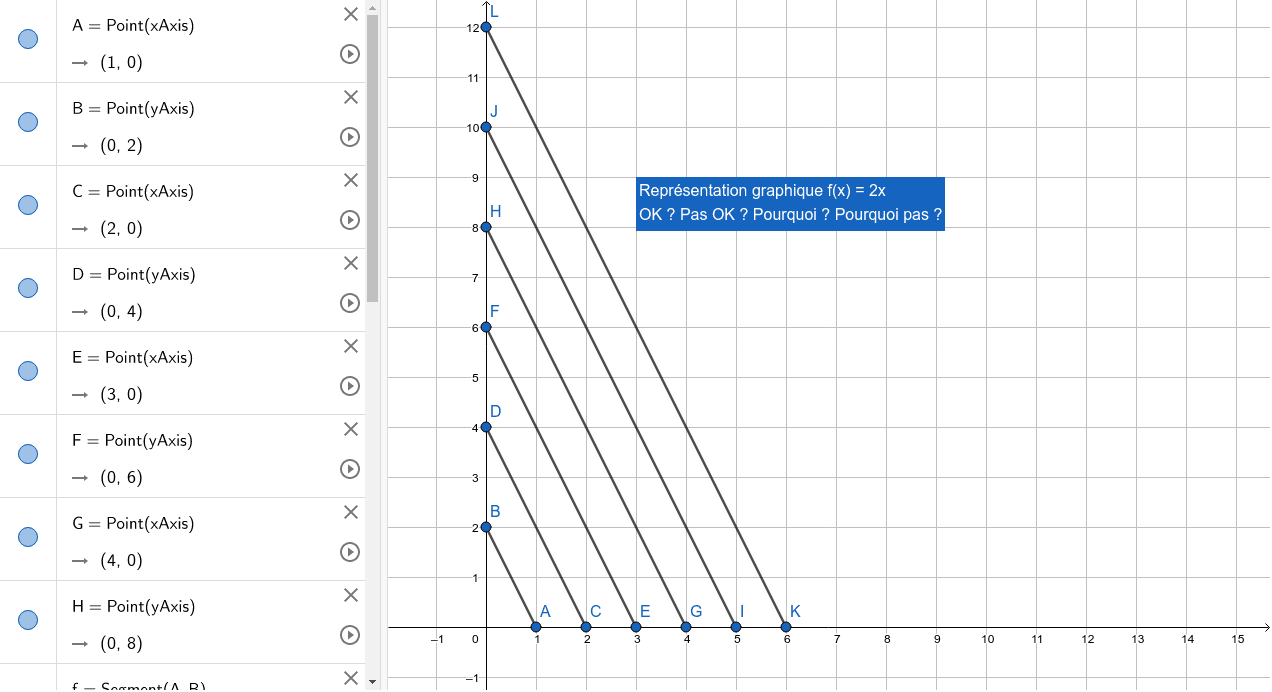



Representation Graphique F X 2x Bis Ok Geogebra
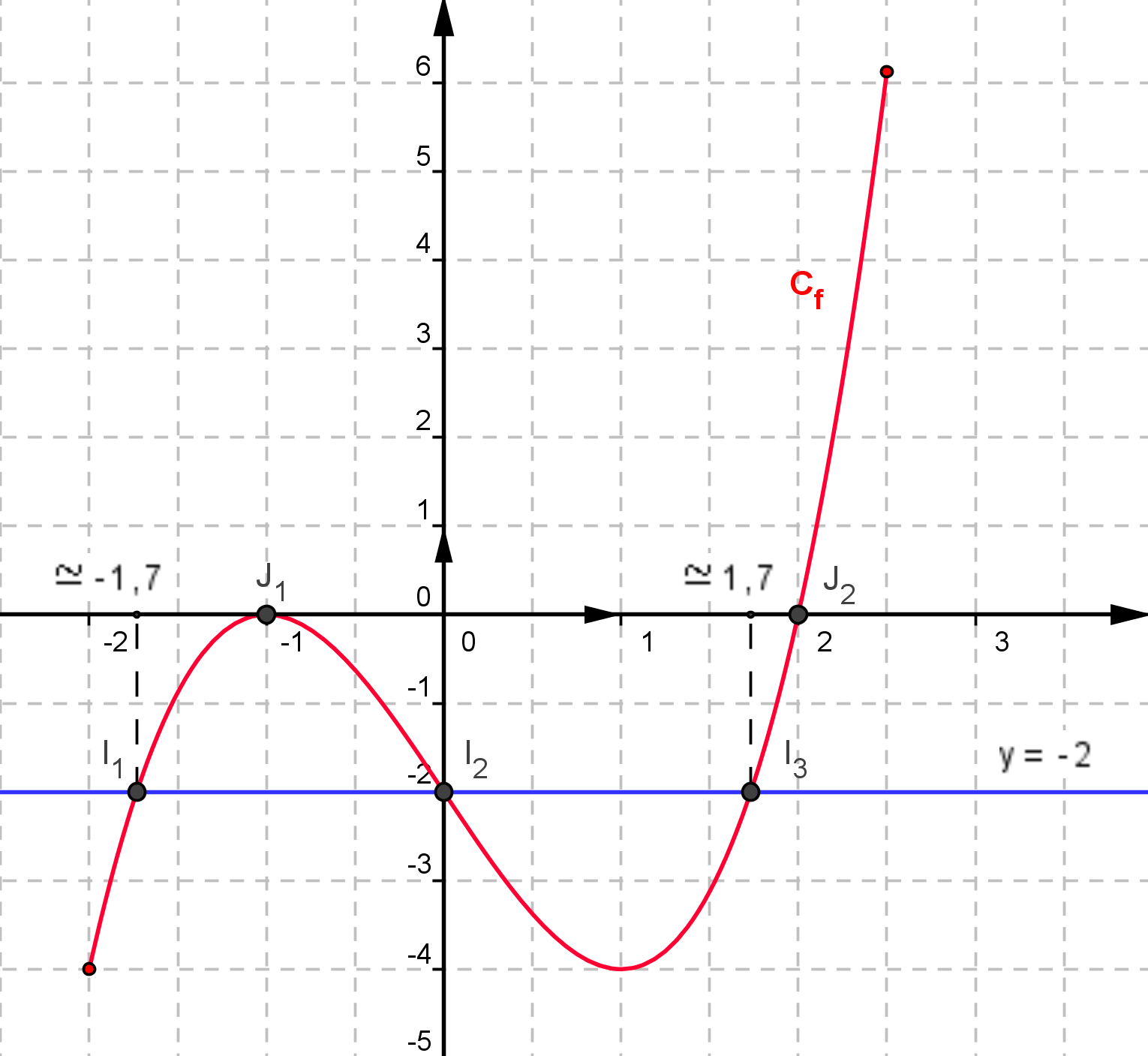



Notion De Fonction Resolution Graphique Fonction Affine Pdf Free Download




Bonjour F Est La Fonction Definie Sur 2 6 Par F X X 4x B Resoudre Graphiquement L Equation Nosdevoirs Fr




Bonjour Pouvez Vous M Aider S Il Vous Plait Mathematiques Premiere Au 1 Il Faut Determiner Nosdevoirs Fr




Calameo Aide Individualisee Sur Les Fonctions Affines




Fonctions Polynomes Et Homographiques 1




La Fonction Carre Fiche De Cours Mathematiques Schoolmouv




La Fonction Racine Carree Fiche De Revisions Pour Seconde L Etudiant
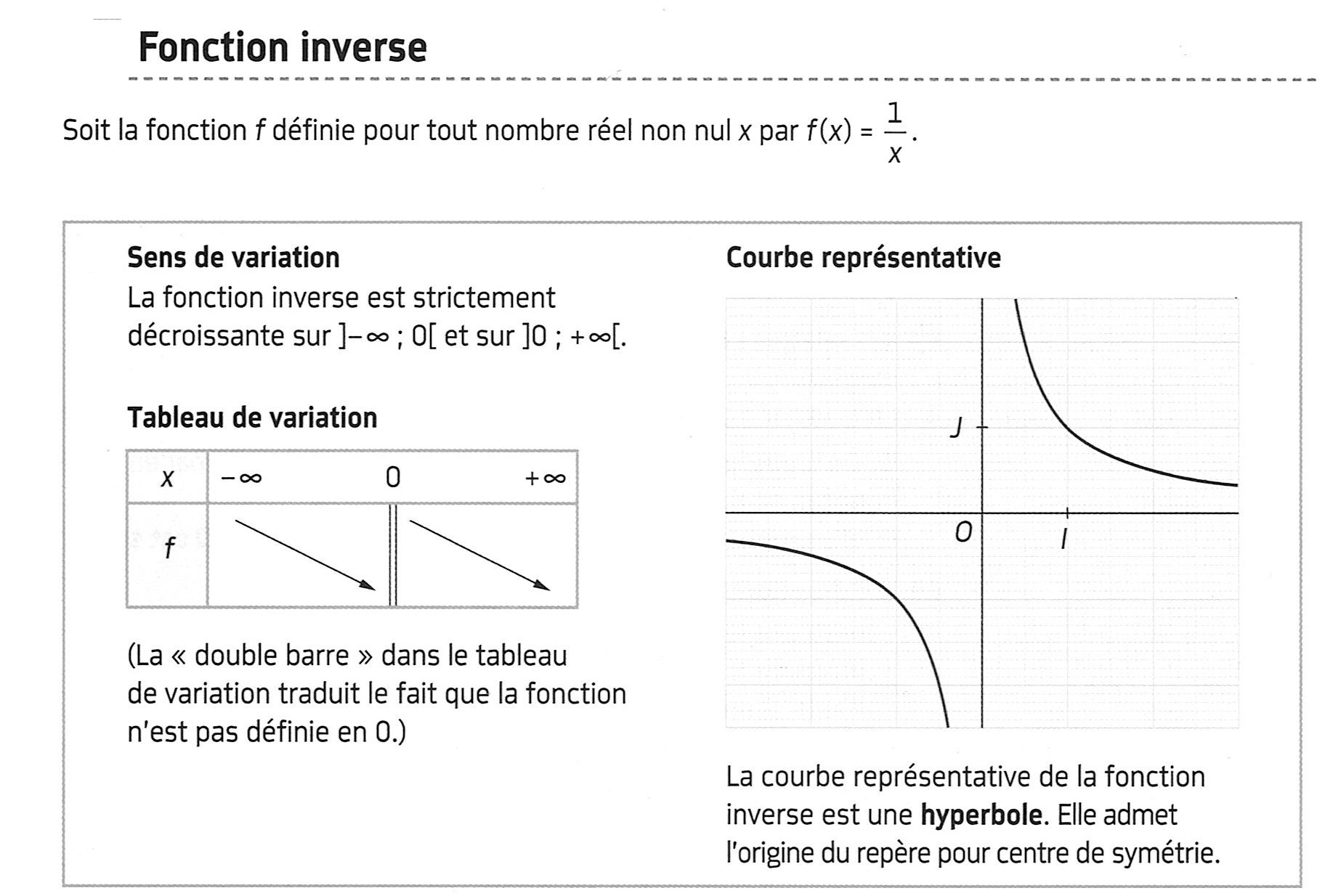



Mathbox Definition Variation Et Representation Graphique D Une Fonction Inverse




Calameo Correction 3 Preparation Brevet Blanc Vacances De La Toussaint
.png)



Lecon Fonctions Affines Tout Savoir Sur Les Fonctions Affines
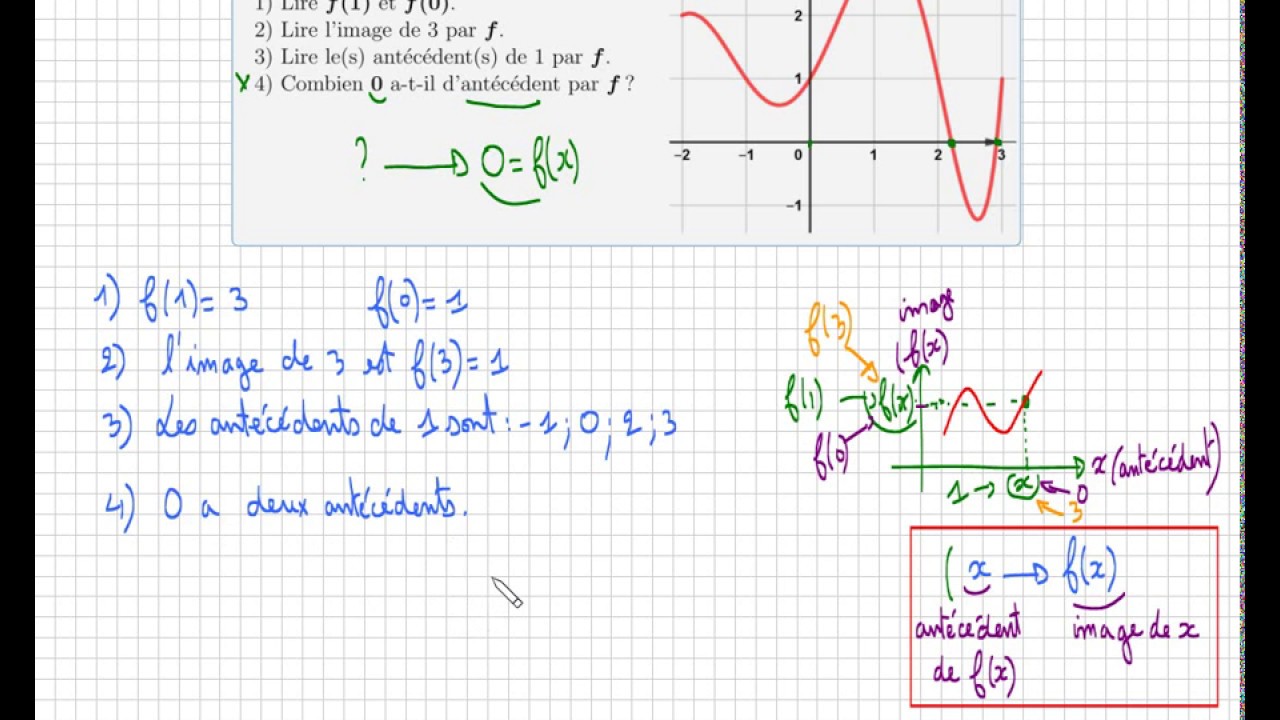



Fonction Exercice Pour Savoir Lire Image Et Antecedent Graphiquement Troisieme Seconde Youtube




Resoudre Graphiquement Une Equation Du Type F X K 2nde Exercice Mathematiques Kartable




Exemple De Resolution Graphique D Une Equation De La Forme F X K Geogebra
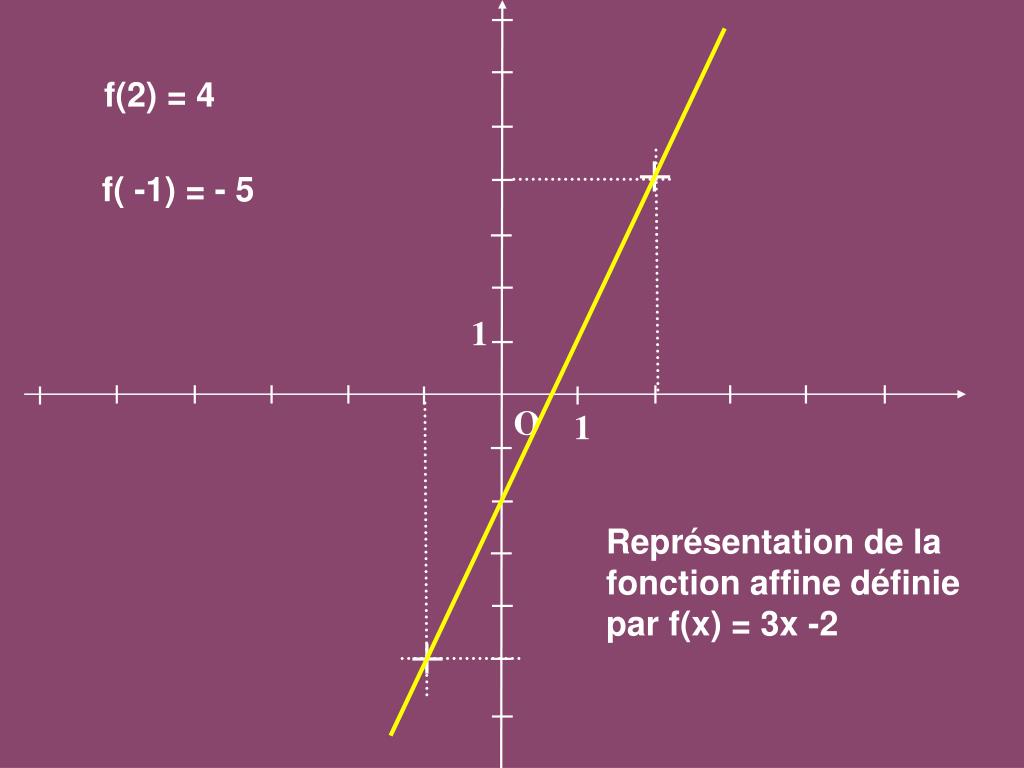



Ppt Representation Graphique D Une Fonction Affine Powerpoint Presentation Id 345




Exercices Types Lectures Graphiques Variations Et Extremums Des Fonctions Lecture Graphique Fonctions Paires Et Impaires Fiche Exercices Maths Seconde




Bonjour J Aimerais De L Aide Pour Un Devoir Maison De Seconde Merci D Avance A Ceux Qui Nosdevoirs Fr




Chapitre Iv Sens De Variation D Une Fonction Resolution Graphique D Inequations Pdf Free Download




Etudier Une Suite Definie Par Relation De Recurrence Avec Des Operations De Fonctions Usuelles Continue Tle Probleme Mathematiques Kartable
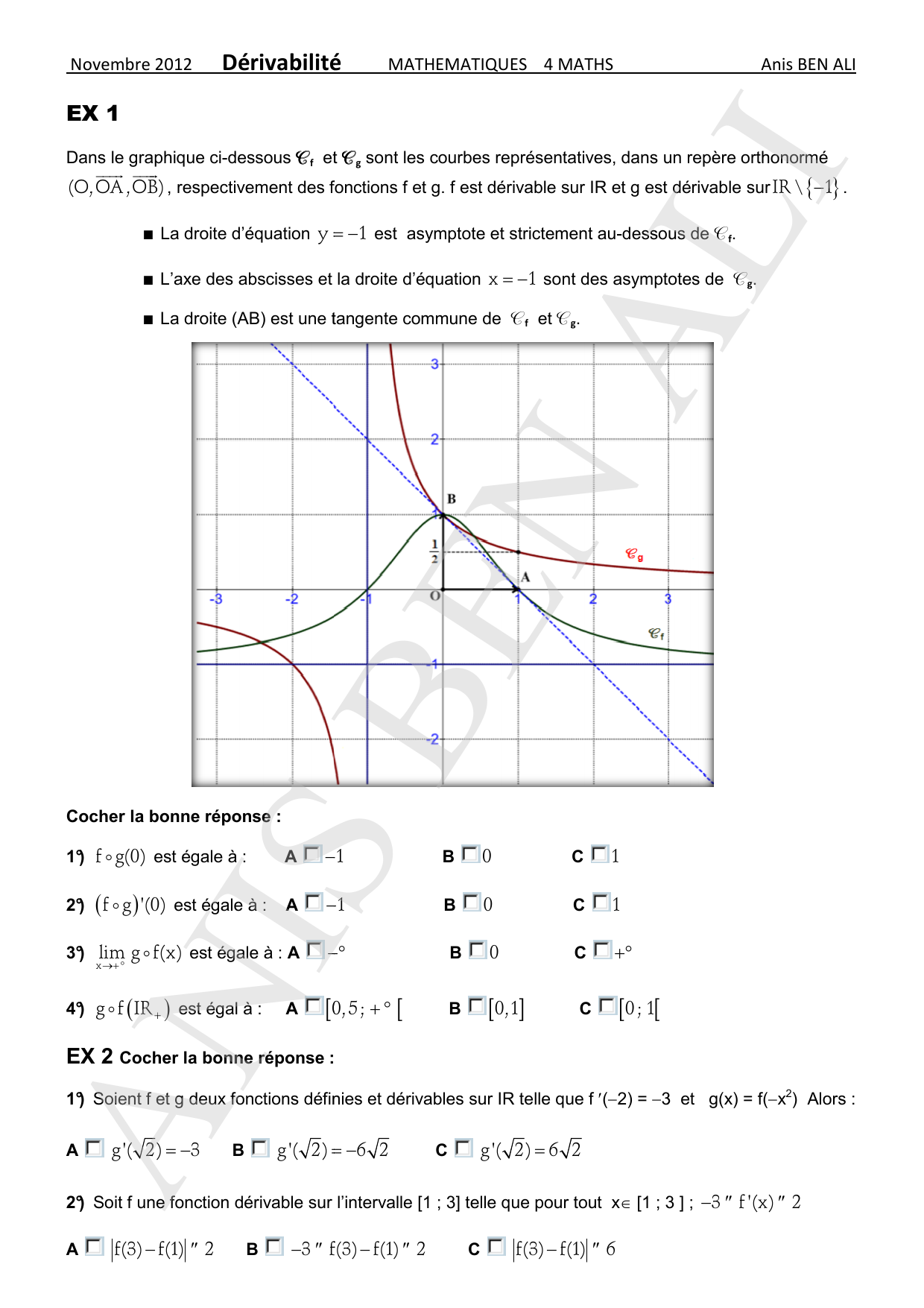



Derivabilite




Niveau 3eme Voici La Representation Graphique D Une Fonction F Pour X Compris Entre 2 Et 8 Nosdevoirs Fr




Lecture Graphique Nombre Derivee Continuite Derivation Lectures Graphiques Et Convexite Fiche Exercices Maths Terminale Es 19



Fonctions Applications Sommaire Ce Document Est Une Introduction A La Theorie Des Fonctions Il Fait Suite Au Doc Ensembles Nous Revenons Aussi Sur Les Proprietes Des Applications Le Doc Raisonnements Est Utile A La Lecture De Certaines Parties De Ce
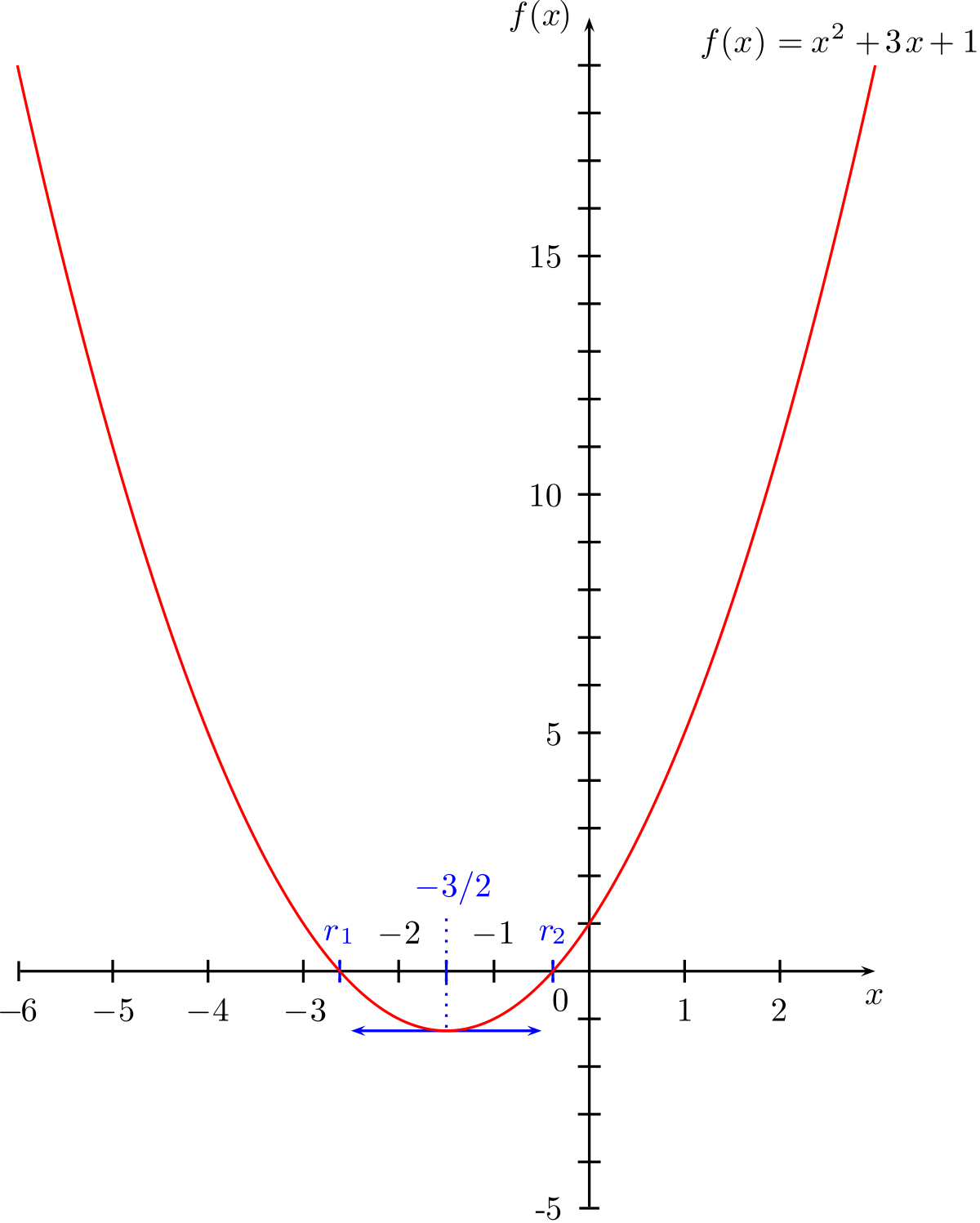



Zero D Une Fonction Wikipedia




1 Lire Sur Le Graphique Les Valeurs De F 0 F 1 F 3 2 Pour Quelles Valeurs De X A T On F X Nosdevoirs Fr
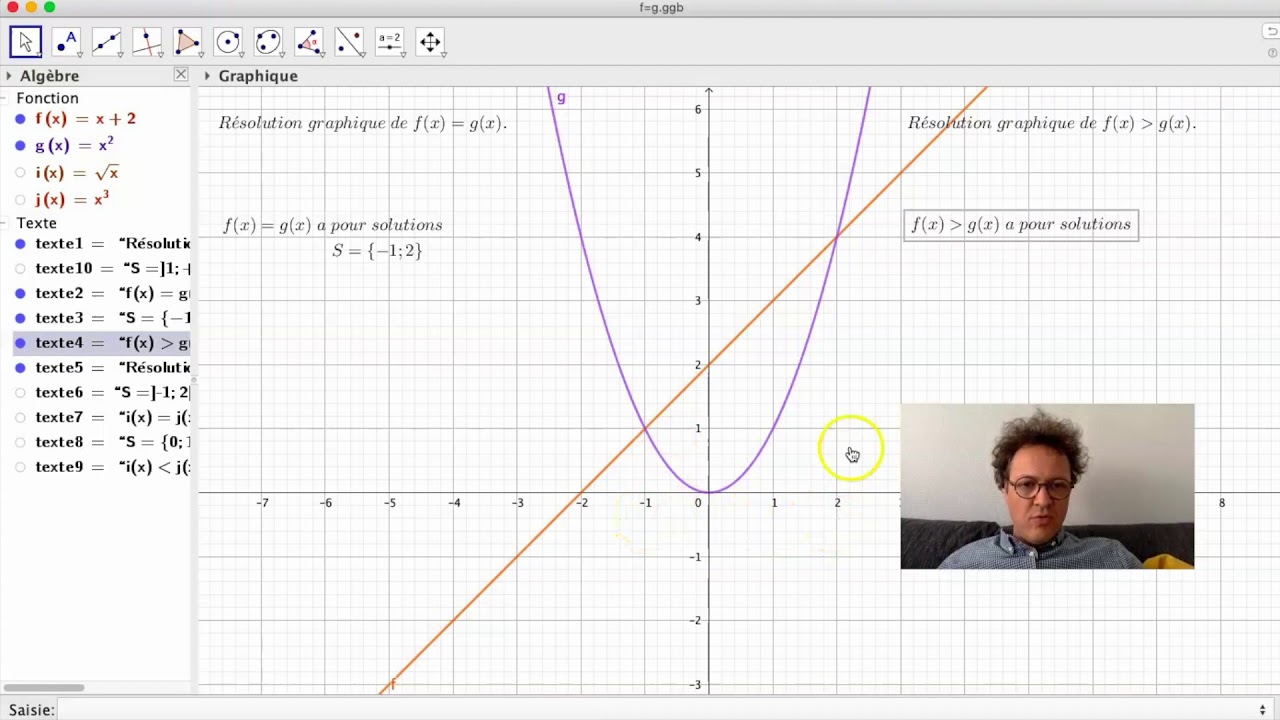



2g Representer Graphiquement Les Fonctions Comment Resoudre Graphiquement F X G X Youtube




Fonctions Exercice Resolution Graphique Equations Inequations Youtube




Resoudre Graphiquement Equation




Fonctions Applications




Cours Les Fonctions Affines Pdf



0 件のコメント:
コメントを投稿